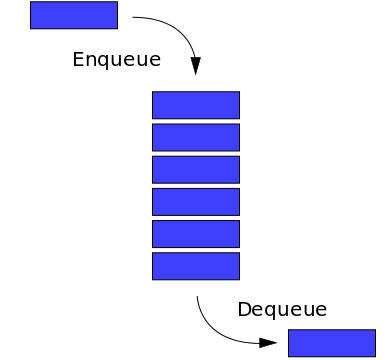
What is a Queue?
The queue is a linear list of data working on FIFO(First In First Out) nature. The Insertion can take place from the Front end and deletion can take place from the Rear end. The process of insertion of an element into a queue is called Enqueue and the process of deletion of an element from the queue is called Dequeue. All operation works in constant time i.e, O(1)
Few important points regarding Queue
- It is a Linear Data Structure
- It follows FIFO: First In First Out algorithm
- The Insertion can be taken place from the rear end.
- The Deletion can be taken place from the front end.
Courtesy: Wikimedia
Insertion of Data into Queue
Deletion of Data from Queue
Java program for Queue
import java.io.*;
class Queue
{
int queue[]; // Array of Queue
int size; // Size of the Queue
int front; // Front element
int rear; // Rear element
int value; // For value
Queue(int size) // Parameterised Constructor
{
this.size = size;
queue = new int[size];
front = 0;
rear = 0;
}
void insert(int value) // Function to insert element in Queue
{
if(rear == size) // Condition for Overflow
{
System.out.println("OVERFLOW");
}
else
{
queue[rear] = value; // Storing value in Queue
rear = rear + 1;
}
}
int delete() // Function to delete element from Queue
{
if(front == 0 && rear == 0) // Condition for Underflow
{
System.out.println("Under flow");
return -999;
}
else
{
value = queue[front]; // Storing the element which will be removed
front = front + 1;
if(front == rear) // Condition for emptying the Queue
{
front = 0;
rear = 0;
}
return value;
}
}
void display() // Function for printing elements in the queue
{
if(front == 0 && rear == 0)
{
System.out.println("The Queue is empty");
}
else
{
System.out.println("The elements in the queue are : ");
for(int i=front; i<rear; i++)
{
System.out.println(queue[i]);
}
}
}
public static void main(String args[])throws IOException
{
int n, value, i;
InputStreamReader in = new InputStreamReader(System.in);
BufferedReader br=new BufferedReader(in);
System.out.println("\nEnter the size of array Queue:");
n=Integer.parseInt(br.readLine());
Queue ob = new Queue(n); // Object create with a parameter
System.out.println("Enter value into Queue:");
for(i=0; i<n ;i++)
{
value=Integer.parseInt(br.readLine());
ob.insert(value);
}
System.out.println("Queue Elements:");
ob.display();
}
}
Sample output:
Enter the size of array Queue:
5
Enter value into Queue:
4
5
3
7
8
Queue Elements:
The elements in the queue are :
4
5
3
7
8
Deletion from Queue:
4 Value is deleted
The elements in the queue are :
5
3
7